L’intérêt peut être déni comme la rémunération d’un prêt d’argent. C’est le prix à payer par l’emprunteur au prêteur pour utiliser un capital pendant une période de temps. Il s’agit d’une dépense pour l’emprunteur et d’un revenu pour le prêteur.
L’intérêt est variable selon la loi de l’offre et de la demande, du montant du prêt, de la durée et du taux d’intérêt. Il y a deux types d’intérêt : intérêt simple et intérêts composé.
Table des matières
Définition d’intérêt simple
Un intérêt simple est utilisé pour des opérations de court terme (qui n’excèdent pas un an).
Lorsque la durée du prêt est de quelques mois, en général l’intérêt sera payé en une seule fois, soit lors de la remise du prêt, soit lors de son remboursement.
Quand le prêt (ou le placement) est fait à intérêts simples), les intérêts dus à la fin de chaque période choisie comme unité de temps (trimestre, semestre ou année) sont calculés sur le capital initial : ils ne sont pas capitalisés pour le calcul des intérêts de la période suivante.
Il est versé en une seule fois au début de l’opération, c-à-d lors de remise du prêt, ou à la n de l’opération c-à-d lors du remboursement. Le montant de l’intérêt dépend de l’importance du capital prêté et de la durée du prêt.
Principe et champ d’application d’intérêt simple
L’intérêt simple se calcule toujours sur le principal. Il ne s’ajoute pas au capital pour porter lui même intérêt.
L’intérêt simple est proportionnel au capital prêté ou emprunté.
L’intérêt simple concerne essentiellement les opérations à court terme (inférieures à un an).
le taux d’intérêt pour une période de moins d’un an est calculé sur la base d’une année de 360 jours (12 mois de 30 jours).
Cette convention contribue à afficher un taux annuel ( i ) légèrement plus faible que s’il était calculé sur la base d’une année de 365 jours.
Le montant de l’intérêt se mesure donc par :
I = V x j x i/360
i/360 représente donc le taux d’intérêt pour un jour
Calcul d’intérêt simple
Soit,
C : le montant du capital prêté ou emprunté (valeur nominale)
t : le taux d’intérêt annuel (en pourcentage )
n : la durée de placement (en année )
I : le montant de l’intérêt à calculer
V : la valeur acquise par le capital (valeur future)
- Formule d’intérêt simple
I = C.t.n / 100
V = C + I
V = C + C ( 1 + (t.n/100) )
- Remarques
Si la durée du placement est exprimée en mois, on aura :
I = C. (t/100) . (n/12)
I = C.t.n/1200
V = C ( 1 + ( t.n/1200) )
Si la durée du placement est exprimée en jours, on aura:
I = C. (t/100) . (n/360)
I = C.t.n/36000
V = C ( 1 + ( t.n/36000) )
- Remarque
Pour le calcul d’intérêt simple , certain utilise une année de 365 jours. Cet intérêt calculé s’appelle intérêt civil.
- Application
Une somme de 10.000 euros est placée sur un compte du 23 Avril au 9 Août au taux simple de 7 %
1. Calculer le montant de l’intérêt produit à l’échéance.
2. Calculer la valeur acquise par ce capital.
3. Chercher la date de remboursement pour un intérêt produit égal à 315 euros.
- Solution
1. On a I = C.t.n/36000, C = 10 000, t = 7
Calculons alors le nombre de jours de placement
Avril : 7
Mai : 31
Juin : 30
Guillet : 31
Août : 9
I = 10 000.7.108 / 36000 = 210 euros
2. La valeur acquise par ce capital est égale à V,
V = C + I = 10000 + 210 = 10210 euros
3. Date de remboursement correspondant à un intérêt de 315 euros
I = C.t.n/36000 donc n = 36 000.I / C.t ⇒ n = 36 000.315 / 10 000.7 = 162 jours
Avril : 7
Mai : 31
Juin : 30
Juillet : 31
Août : 31
Septembre : 30
Octobre : 2
Date de remboursement : 2 octobre
Taux moyen d’une série de placement simultanés
Soit J opérations de placement simultanées à intérêt simple de sommes Cj, aux taux tj, sur nj jours.
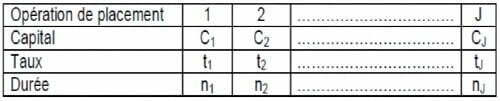
Le taux moyen de cette série de placement est un taux unique Taux qui, appliqué à cette même série, permet d’obtenir le même intérêt total. L’intérêt total de cette série est égal à :
I = C1.t1.n1 / 36 000 + C2.t2.n2 / 36 000 + ……….. + Cj.tj.nj / 36 000
D’après la définition, le taux moyen de placement sera calculé par la résolution de l’égalité suivante :
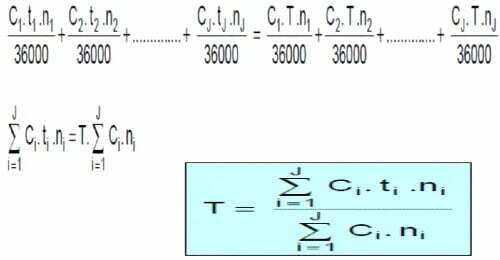
- Application
Calculer le taux moyen de placement des capitaux suivants :
2000 euros placés à 3% pendant 30 jours,
3000 euros placés à 4% pendant 40 jours
4000 euros placés à 5% pendant 50 jours.
- Solution
T = ( 2 000.3.30 + 3 000.4.40 + 4 000.5.50 ) / ( 2 000.30 + 3 000.40 + 4 000.50 ) = 4,37%
Les méthodes commerciales de calcul d’intérêt simple
Méthode des nombres et des diviseurs fixes
On part de la formule : C.t.n / 36 000
n étant exprimé en jours. divisons par t les deux membres, on obtient :
( C.t.n / t ) / ( 36 000 / t ) ou encore C.n / ( 36 000 / t)
Si nous posons C.n = N et 36 000 / t = D, alors la formule peut s’écrire : I = N / D
N étant le nombre et D le diviseur fixe.
- Application
Quel est l’intérêt global des capitaux suivants placés à 12 % ?
68 000 pendant 45 jours
45 250 ˶˶ 96
29 750 ˶˶ 147
15 760 ˶˶ 265
36 148 ˶˶ 36
26 855 ˶˶ 128
Tableau de calcul :
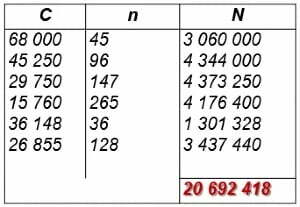
Calcul du diviseur fixe D = 36 000/t = 36 000/12 = 3 000
d’où N/D = 20 692 418/3 000 = 6 897,47
Méthode du soixante
Cette méthode est utilisée lorsque le taux de base ne permet pas une division exacte de 36 000.
Terme échu ,à échoir, taux effectif
les intérêts peuvent être versés en début ou en fin de période :
Lorsque les intérêts sont payés en fin de période, on dit qu’ils sont post-comptés ou terme échu. Ils sont calculés au taux d’intérêt simple, sur le capital initial C qui représente le nominal. Ils sont ajoutés ensuite, au nominal pour constituer le capital final V (valeur acquise).
on a donc:
V ――――⏵V+I
V = C ( 1 + ( t.n / 36 000 ) )
Lorsque les intérêts sont payés en début de période, on dit qu’ils sont précomptés ou terme à échoir. Ils sont calculés sur le nominal, qui constitue la somme finale C et retranchés du nominal pour déterminer la somme initiale ou mise à disposition.
Etant donné un nominal égal à C, on aura : C’ = C – I, où C’ désigne la somme initiale.
Quand les intérêts sont payables d’avance, le taux d’intérêt effectif est celui appliqué au capital effectivement prêté ou emprunté C’ donne le montant de l’intérêt produit. En désignant par T, le taux effectif, on aura alors
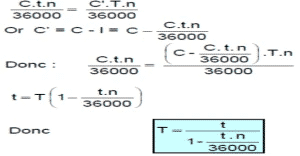
- Remarque
– Une somme V empruntée sur j jours au taux i précompté ne donne lieu au début de l’opération qu’à un versement de : V-V0 = I A l’échéance, l’emprunteur devra rembourser V.
– L’intérêt précompté avantage le prêteur puisqu’il reçoit l’intérêt plus tôt, au début de la période de placement.
– L’intérêt postcompté avantage l’emprunteur puisqu’il verse l’intérêt plus tard, à la fin de la période d’emprunt.
- Application
Une personne place à intérêts précomptés la somme de 30000 euros pour une durée de 6 mois au taux de 10 %. Quel est le taux effectif de ce placement ?
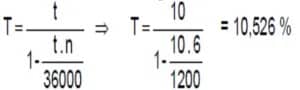
V. Calcul des facteurs de l’intérêt simple
Les facteurs de l’intérêt simple sont : le capital, le taux et la durée.
calcul du capital
Il s’agit de la somme placée ou prêtée à une date déterminée
De la formule générale I = C.t.n / 36 0000 on tire C = 36 000. I / t.n
- Exemple :
Quel est le capital ,qui , placé à 10% pendant 75 jours rapporterait 406.25 euros ?
C ═ 36 000.406,25 / 10.75 = 19 500 euros
La valeur acquise
Pour comparer ou additionner des sommes versées ou reçues à des dates différentes, il est nécessaire d’ actualiser afin de les ramener en théorie à la même date.
L’actualisation consiste à calculer la valeur aujourd’hui, (la valeur actuelle) d’une somme à recevoir à une date future.
La capitalisation consiste à calculer la valeur à une date future, que l’on appelle valeur future ou valeur acquise, d’une somme versée aujourd’hui.
On appelle valeur acquise par un capital placé pendant un certain temps, la valeur du capital augmentée des intérêts à la fin de la période de placement.
Soit V : la valeur acquise par le capital à la fin de la période du placement
V= C + I
- Application
Quelle est la valeur acquise par un capital de 120 000 euros
placé à 12.5 % pendant 126 jours ?
- Solution
I = 120 000 x 12.5 x 126 / 36 000 = 5 250
V = 120 000 + 5 250 = 125 250 euros
Le cas des intérêts postcomptés
1. Valeur acquise ou valeur future d’un capital V0, à intérêt postcompté
La valeur acquise ou valeur future d’un capital V0 placé au taux i pendant j jours est égale à la valeur initiale de ce capital augmenté de la valeur des intérêts.
VF = V0 x (1 + i x j /360)
- Application
Un capital de 5.000 euros a été placé à intérêt simple au taux de 5,5 % le 1er octobre. Quelle est sa valeur acquise le 10 novembre ?
- Solution
Il y a 40 jours entre le 1er octobre et le 10 novembre.
VT = 5.000 x (1 + 5,5 % x 40/360) = 5 030,56 euros.
2. Valeur actuelle d’un capital VF à recevoir dans j jours, à intérêt postcompté
Pour calculer la valeur actuelle d’un capital, on utilise un procédé inverse à celui utilisé pour calculer la valeur future :
V0 = VF / (1 + i x j /360)
- Application
Quelle est la valeur actuelle, au taux d’actualisation de 5 %, d’un capital de 500 euros à recevoir dans 25 jours ?
- Solution
V0 = 500 / (1 + 5% x 25/360) = 498,27 euros.
Le cas des intérêts précomptés
1.Valeur actuelle d’une somme VF à payer ou à recevoir dans j jours au taux i précompté
La valeur actuelle d’une somme VF à recevoir ou à payer dans j jours au taux i précompté est égale à la valeur de cette somme diminuée de la valeur des intérêts.
V0 = VF x (1 – i x j /360)
- Application
Une entreprise émet sur le marché monétaire des billets de trésorerie d’un montant nominal de 150 000 euros, d’échéance 90 jours et de taux 3,5 % précompté.
Quel est le prix d’émission du billet de trésorerie ?
- Solution
V0 = 150 000 x (1 – 3,5 % x 90 / 360) = 148 687,50 euros
2. Valeur acquise par une somme V0 placée ou empruntée sur j jours au taux i précompté
Pour calculer la valeur acquise d’une somme V0 placée ou empruntée à taux précompté, on utilise un procédé inverse de celui utilisé pour calculer la valeur actuelle :
VF = V0 / (1 – i x j /360)
- Application
Une entreprise a besoin d’un financement d’au moins 30 000 000 et souhaite émettre sur le marché monétaire des billets de trésorerie de valeur nominale 150 000 euros, d’échéance 180 jours et de taux facial 4,5 % précompté. Combien de billets de trésorerie doit-elle émettre ?
- Solution
Si l’entreprise émettait 200 billets de trésorerie
(30 000 000 / 150 000), elle n’obtiendrait aujourd’hui qu’un financement de :
30 000 000 (1 – 4,5 % x 180 /360) = 29 325 000 euros.
Pour obtenir au moins 30 000 000 euros, elle doit donc emprunter un montant correspondant à la valeur future des 30 000 000 euros dont elle a besoin aujourd’hui : VF = 30 000 000 / (1 – 4,5 % x 180 /360) = 30 690 537,08 euros.
Les billets de trésorerie étant d’une valeur nominale de 150 000 euros, il lui faudra émettre 205 billets pour obtenir un peu plus de 30 millions de euros
Calcul de la durée
De la formule générale I = C.t.n / 36 0000 on tire n = 36 000. I / t.C
- Application
Pendant combien de temps un capital de 45 000 doit-il être placé à 11.5% pour générer 805 euros d’intérêts ?
n = 805.36 000 / 45 000.11,5 = 56 jours
Calcul du taux d’intérêt
Le taux d’intérêt peut dépendre de plusieurs facteurs :
– loi de l’offre et de la demande des capitaux
– degré de confiance du prêteur envers l’emprunteur ;
– durée du prêt ;
– conjoncture économique et sociale.
De la formule générale I = C.t.n / 36 0000 on tire t = 36 000. I / C.n
- Application
Un capital de 28 600 euros placé pendant 85 jours a rapporté 607.75 euros. Calculer le taux ?
- Solution
t = 36 000. I / C.n = 607,75.36 000 / 28 600.85 = 9%
L’escompte
L’escompte est une opération de crédit par laquelle la banque transforme une créance, matérialisée par un effet de commerce, en liquidité au profit de son client, avant son échéance et contre remise de l’effet.
- L’escompte commercial
C’est l’intérêt simple calculé à un taux indiqué par le banquier sur une somme égale à la valeur nominale de l’effet et une durée allant du jour de la négociation jusqu’au jour de l’échéance
Soit,
V : la valeur nominale de l’effet, c’est la valeur de l’effet à son échéance
t : taux d’escompte
n : durée de l’escompte, c’est le nombre de jours séparant la date de négociation de l’effet de sa date d’échéance.
e : l’escompte commercial
e = V.t.n / 36 000
- Application 1
Calculons l’escompte d’un effet de 40 000 euros au 31 juillet remis à l’escompte le 26 juin. Taux 11,25 %.
Nombre de jours : du 26 juin au 30 juin 4 jours
jusqu’au 31 juillet 31 jours
= 35 jours
e = 40 000 x 11,25 x 35 / 36 000 = 437,50
ou
D = 36 000 / 11,25 = 3 200e = 40 000 x 35 / 3 200 = 437,50
- Application 2
Calculer l’escompte commercial d’un effet de valeur nominale de 8 300 euros à 40 jours au taux de 10, 75 %.
e = 8 300 x 40 x 10.75 / 36 000 = 99.14
Valeur actuelle
C’est la valeur que le banquier doit verser au porteur de l’effet à l’occasion de l’opération d’escompte. Elle représente la différence entre la valeur nominale et l’escompte retenu par le banquier.
En désignant par a cette valeur actuelle on aura :
On a : e = V.t.n / 36 000 et a = V – e
- Reprenons l’application 1
On obtient : a = 40 000 – 437.50 = 39 562.50
Calcul de la valeur actuelle (a) en fonction de la valeur nominale (V)
a = V – e
a = V – ( V.t.n / 36 000 )
a = V ( 1 – ( t.n / 36 000 ) )
a = V ( (36 000 – t.n) /36 000 )
Calcul de l’escompte (e) et de la valeur actuelle (a) en fonction du diviseur (D)
Si on note par D = Diviseur = 36 000 / t
On aura : e = V.n/D
a = V – e
a = V – V.n/D
a = ( V (D – n)) / D
Calcul de l’échéance, du taux, de la valeur nominale
- L’échéance
Quel est le nombre de jours jusqu’à l’échéance d’un effet de 4 800 euros qui est escompté au taux de 12 % l’an à une valeur actuelle de 4 720 euros ?
Reprenons la formule : a = V – e
on peut écrire : 4 720 = 4 800 – e donc e = 80
on peut écrire encore : e = V .t.n / 36 000 = 80
d’où 4 800 x 12 x n / 36 000 = 80
4 800 x 12 x n = 80 x 36 000
57 600 n = 2 880 000
n = 50 jours.
- Taux d’escompte
Quel est le taux qui a été appliqué à un effet de valeur nominale 780 euros pendant 35 jours et ayant une valeur actuelle de 771,66 euros .
On peut écrire : 771.66 = 780 – e donc e = 8.34
d’où 8.34 = V .t.n / 36 000
8.34 = 780 x 35 x t / 36 000
36 000 x 8.34 = 780 x 35 x t
300 240 = 27 300t
t = 11 donc taux = 11 % l’an.
- Valeur nominale
Quelle est la valeur nominale d’un effet qui, escompté au taux de 11 % l’an pendant 54 jours a une valeur actuelle de 1 983.50 ?
On peut écrire : 1 983.50 = V – Vtn / 36 000
d’où 1 983.50 = V – V x 11 x 54 / 36 000
1 983.50 = V – 0.0165V
1 983.50 = 0.9835V
V = 2 017 euros
L’intérêt simple PDF
| L’intérêt simple en PDF | Télécharger |




parfait