L’analyse des caractéristiques des préférences du consommateur montre la possibilité de phénomènes d’indifférence : différentes combinaisons de consommation peuvent entraîner un identique niveau de satisfaction. C’est ce phénomène qu’exprime graphiquement la courbe d’indifférence.
On appelle courbe d’iso-satisfaction ou isophélime la courbe qui représente le niveau de satisfaction commun généré par différentes combinaisons de consommation de biens A et B.
Table des matières
Définition d’une courbe d’indifférence
« Une courbe d’indifférence représente toutes les combinaisons de paniers de biens qui procurent au consommateur la même satisfaction. L’individu est dès lors indifférent entre les divers paniers représentés sur la courbe ».
Une courbe d’indifférence est une représentation géométrique représentant des combinaisons de biens qui assurent au consommateur le même niveau de satisfaction..
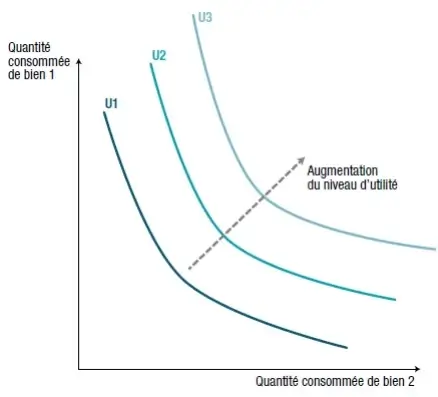
Le schéma représente des cartes d’indifférences. Chaque courbe représente un niveau d’utilité donnée, U1, U2 et U3, plus on s’éloigne de l’origine, plus le niveau d’utilité augmente.
Cette augmentation de l’utilité est justifiée par l’axiome de la non saturation (plus la quantité consommée augmente, plus le niveau d’utilité augmente). Les biens consommés sont des biens utiles, rares et disponibles en vertu de l’hypothèse de la certitude de l’information.
Représentation graphique de la courbe d’indifférence
Une courbe d’indifférence est construite à partir d’une fonction d’utilité ordinale.
Exemple
Considérons un consommateur dont les préférences sont représentées par les données suivantes :
U(x, y) = x y
Pour une utilité représentée par un indice ordinale de 400 par exemple, on aura :
y= 400 / x
Si x=1, y=400
Et si Y= x=400
Ainsi les couples de biens (1, 00), (400, 1) et (200, 2) représentent la même utilité pour le consommateur car situés sur une même courbe d’indifférence.
Les propriétés des courbes d’indifférences
- Les courbes d’indifférence ne se coupent jamais
Cela voudrait dire que les courbes n’admettent jamais un point d’intersection. Cette propriété est relatée par l’axiome de transitivité. En effet, en considérant que deux courbes d’indifférences admettent un point d’intersection, on aurait la forme suivante :
D’après le schéma, les points qui se retrouvent sur la même courbe procurent au consommateur le même niveau de satisfaction, il en est ainsi des points A1 et A2 sur la courbe UA et également des points A1 et B2 sur la courbe UB.
Cependant, si l’on se réfère à l’axiome de la non saturation, le point B2 serait préféré par le consommateur que le point A2, car il permet de consommer plus de quantité de biens x et y. par conséquent, deux courbes d’indifférence ne se croisent jamais.
- Les courbes d’indifférence sont toujours décroissantes
Au niveau mathématique, cela veut dire qu’une courbe d’indifférence a toujours une pente négative. Sur le plan économique, ceci est relatif à l’hypothèse de la substituabilité des biens.
Le consommateur ne peut augmenter la consommation d’un bien sans pour autant réduire celle d’un autre bien qui lui est substituable. Cette décroissance est également le résultat de l’axiome de la non-saturation.
Menons un raisonnement par absurde et considérons des courbes d’indifférence croissantes : Cela voudrait dire que les couples de biens situés en haut seront préférés par le consommateur car assurant des quantités consommées de biens plus importantes.
Il s’ensuit que les courbes d’indifférence ne peuvent être que décroissantes.
- Les courbes d’indifférence sont toujours convexes par rapport à l’origine.
Les courbes d’indifférences se situent donc au-dessus de leurs tangentes. Cette convexité est liée à la substitution entre les biens. L’augmentation de la consommation d’un bien ne peut se faire que si elle est compensée par la baisse d’un autre bien qui lui est substituable.
- La densité des courbes d’indifférence.
Cette propriété signifie que quelque soit un panier de consommation sur un plan à feux dimensions, ce panier appartient à une courbe d’indifférence.
Exercice corrigés sur la courbe d’indifférence
Soit un consommateur qui consomme seulement deux biens X et Y. Ses préférences peuvent être représentées par la fonction d’utilité suivante: U = (1/4)X²Y. Ce consommateur dispose d’un revenu R qu’il alloue en totalité à l’achat de ces deux biens. Soit Px et Py les prix des biens X et Y.
TAF : Supposons que le niveau d’utilité soit fixé à U0 =16, donnez l’équation de la courbe d’indifférence de ce consommateur et tracez-la.
Solution
Nous avons la fonction d’utilité : U = (1/4)X²Y
Pour U0 =16, nous obtenons : (1/4)X²Y =16. d’où: Y = 64 / X² , l’équation de la courbe d’indifférence.
Pour tracer la courbe d’indifférence, nous donnons des valeurs à X et en fonction de ces valeurs nous déterminons Y. Pour X=1, Y=64 ; pour X=2, Y=16 : pour X=4, Y=4. Le graphique a la forme suivante:
La courbe d’indifférence PDF
| La courbe d’indifférence en PDF | Télécharger |